Кроме того, можно было бы присвоить имя каждой яме, но такое решение является неподходящим по другой причине: нам нет смысла проводить различия между ямами. Гораздо проще использовать унарный предикат Pit, который принимает истинное значение в квадратах, содержащих ямы. Наконец, поскольку имеется точно один вампус, для его представления равным образом подходят и константа Wumpus, и унарный предикат (а последний способ обозначения с точки зрения вампуса может даже оказаться более почетным). Вампус проживает точно в одном квадрате, поэтому для именования этого квадрата целесообразно использовать функцию, такую как Ноте {Wumpus). Это позволяет полностью избежать необходимости применения громоздкого множества высказываний, которые требовались в пропозициональной логике для обозначения того, что вампус находится точно в одном квадрате. (А при наличии двух вампусов ситуации в пропозициональной логике стала бы еще хуже.)

Местонахождение агента меняется со временем, поэтому мы будем применять запись At {Agent, s, t) для указания на то, что агент находится в квадрате s во время t. Зная свое текущее местонахождение, агент сможет выявлять путем логического вывода свойства текущего квадрата на основании данных о свойствах его текущего восприятия. Например, если агент находится в некотором квадрате и чувствует ветерок, то в этом квадрате чувствуется ветерок: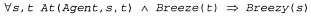

Нам требуется знать не то, что агент вообще почувствовал ветерок, а то, что ветерок чувствуется в определенном квадрате, поскольку известно, что ямы не могут менять своего местонахождения. Обратите внимание на то, что предикат Breezy ("в квадрате чувствуется ветерок") не имеет параметра с обозначением времени.

Обнаружив, в каких местах чувствуется ветерок (или неприятный запах), а также, что очень важно, в каких местах не чувствуется ветерок (или неприятный запах), агент получает возможность определять логическим путем, где находятся ямы (и где находится вампус). Существуют два описанных ниже типа синхронных правил, которые позволяют делать такие логические выводы.

• Диагностические правила

Диагностические правила ведут от наблюдаемых эффектов к раскрытию скрытых причин. В очевидных диагностических правилах, касающихся поиска ям, утверждается, что если в квадрате чувствуется ветерок, то в некотором соседнем квадрате должна находиться яма, таким образом:

С другой стороны, если в некотором квадрате не чувствуется ветерок, то ни в одном из соседних квадратов не находится яма: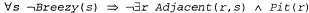